Hey,
Our work on Binary Disassembly Pattern Analysis has been made a US Defensive patent publication. If you are interested, you can read more about it here: http://ip.com/IPCOM/000231860
Cheers!
Finding the square root (of a perfect square) using binary search c#
Well, the logic is pretty straightforward. We start a binary search from a range of 0 to NUM, where NUM is the number whose root we are looking for. Each time, we calculate the middle item of the range and see if it is the square root. If not, we search further either in the right side or the left side of the mid item depending on whether the mid^2 is lesser or greater than NUM.
double GetRoot(double Num,double High=0, double Low=0)
{
if(High<Low || High-Low==1) return -1; //End case
if(High==Low && Low==0) High=Num; //Start case
int Mid= Low+((High-Low)/2);
if(Mid*Mid==Num) return Mid;
else
{
if(Mid*Mid>Num) return GetRoot(Num,Mid,Low);
else if(Mid*Mid<Num) return GetRoot(Num,High,Mid);
}
}
If you have thoughts/ suggestions, post em on comments.
N Queens problem
Well, I can’t possibly have an ‘algorithm of the day’ thread without solving the all famous N QUEENs problem.
Problem description:
Place the maximum amount of Queens on an N by N chess board and print the possible arrangements
Solution:
We will be placing 1 queen at a time per row. We would start from the left most end of the row and move 1 step to the right if there is a collision. We keep doing this till we find a spot that does poses no collisions. If there is no such spot, then one of the previous queens must be moved elsewhere.
Code:
//NQueen problem
#include
using namespace std;
int N;
int Pos=0;
void NQueenDroid(int Board[100], int Remaining)
{
if(Remaining==0)
{
//found a solution
cout<<endl;
for(int i=0;i<N;i++) cout<<Board[i]<<" - ";
Pos++;
return;
}
int Cur= N-Remaining; //placement of current queen
for(int i=0;i<N;i++)
{
bool IsColliding= false;
for(int k=0;k<Cur;k++)
{
//Collision in columns
if(Board[k]==i) {IsColliding=true; break;}
if(abs(Board[k]-i)==abs(Cur-k))
{IsColliding=true; break;} //Collision in diagonals
}
if(IsColliding) continue;
Board[Cur]=i; //place queen
NQueenDroid(Board,Remaining-1);
}
}
int main()
{
N=0;
cout<<"Enter the board size :";
cin>>N;
int Board[100]={0};
NQueenDroid(Board,N);
//End of code
return 0;
}
Dijkstra’s Algorithm
Hi, I’m revamping my algo skills and thought of putting up the code in my blog for fun and for other’s reference. Following is the Dijkstra’s Algorithm, which is used to find the shortest path to all nodes of a graph from a single selected node.
HyperV Annoyance: HyperV hangs at “Loading snapshots for the selected Virtual machine…”
I hit this issue when I upgraded my Hyper-V from Windows Server 2008R2 to Windows Server 2012. Some of the saved VMs were not starting up and Hyper-V failed to even enumerate the saved states of the VMs.
You can work around this issue as follows:
- Right click on the VM node and select Delete Saved State…
- The Incorrect state would be deleted and the VM would be turned off
- Now Right click and select Start.
This fixed the issue on my setup.
Running DHCPerf on Ubuntu
DHCPerf is an open source load testing tool for DHCP-Server setups. The tool is capable of generating DHCP Client traffic with a customizable load. It comes in handy in stress testing scenarios.
I have tested it to work with Ubuntu 12.0 and Nomium’s DHCPerf 1.0.
Steps:
- Download the Red Hat Linux Enterprise Server ES3 (x86) version of DHCPPerf from here: http://www.nominum.com/support/measurement-tools/
- We need the Alien tool to convert the download RPM format file to debian package to be installed in Ubuntu.
- Download Alien tool by running:
$sudo apt-get install alien
- Convert the downloaded RPM file to Debian package format through Alien using the following command
$sudo alien -k DHCPPerf1.0.1.0.rpm
- The Converted Debian package would be placed in the same folder. Install it using the following command:
$sudo dpkg -i DHCPPerf1.0.1.0.deb
- The DHCPerf, by default, gets installed into /usr/local/nom/…
- To Run, navigate into the bin folder under nom and run the DHCPerf command:
./dhcperf –help
to see the usage of the command.
Run WireShark and set the filter to bootp to see the DHCP packets on the wire.
HyperV Annoyance: An error occurred while attempting to snapshot the selected virtual machine – Access denied : Solution
I recently moved to Windows 8 and one of its best features is the Hyper-V role on the client SKU. At times, when I import VHDs from my friends and try to create a snapshop, the HyperV throws an error saying “An error occurred while attempting to snapshot the selected virtual machine: Access denied”
This is because of an ACL mis-configuration and can be fixed in a jiffy.
Note: This is my quick and dirty method of fixing the issue. Not sure if it is the recommended one.
Solution:
- Login as the administrator of the machine
- Right click on the folder in which you have placed the VHD and click on Properties
- Go to Security tab and click on Advanced
- Click on Enable Inheritance and check “Replace all child object permission entries with inheritable permission entries from this object“
- Click Apply
This should resolve the security permission issue.
Microsoft Interview Questions
Hi all!
I recently attended an interview at Microsoft IDC. I have done my best to recollect most of the interview questions. Hope they help
Round 1: Written Test
Time: 75 Minutes
Question 1:
Define a macro that takes the structure name and member name & returns the offset of the member . One must not create any instance of the struct.
Struct T
{
int a;
double b;
inc c;
}
Example:
assume int size as 4 and double as 8
OFFSET(T,a) gives 0
OFFSET(T,b) gives 4
OFFSET(T,c) gives 12
…..
Question 2:
Find the bugs in the following program which tries to delete a node from a singly linked list. Correct the bugs (logical) and optimize the program as much as possible.
struct _NODE
{
_NODE *next;
}
void deletenode(_NODE *head,_NODE n)
{
_NODE *prev,*curr;
prev=head;
curr=head;
while(curr)
{
if(curr==n)
{
delete curr;
prev->next=curr->next;
}
prev=curr;
curr=curr->next;
}
}
Question 3:
An array A contains a series of n numbers both positive and negative. Write a program to find the set of contiguous numbers that give the maximum sum. Also print the lowest and highest index of the series.
Example:
For the array: -1 -2 4 7 -3 1, the Maximal sum is 11: from 2 to 3
- Write solid code and optimize it.
- Complexity must be O(n^2)
Question 4:
Assume a scenario where a company has several data centers at different places in India like Hyderabad Pune etc. It has its main server at some place. Now when file is requested following operation:
- Client from Pune requests a file from the main server
- Server verifies the client
- Main server then forwards the file to the local server.
- Next time when a file is requested from Pune the request is forwarded to the local pune server and client is served from there.
- Write the test cases for it (as much as you can. Anything above 25 will do)
- Analyze the situation and identify all possible breakdown conditions
- How do you rectify the breakdowns?
- How do you carry out authentication?
- Algorithamize your solutions and optimize the same.
Example:
If the local pune server fails the main server must be able to acknowledge the failure and must be able to serve the user seamlessly without any interruptions
Question 5:
Assume that you want to port your favorite mobile application to a mobile platform. What all features would you include? Tell about the various scenarios possible and the different models that can be used. Draw a screen shot and flow diagram for all possible scenarios that you could come up with. Optimize all solutions.
Technical Interviews
The Technical interviews lasted for around 2 hours each and the questions were fired by developing on the answers of the preceding questions. I’ve pulled as much as I could from my memory.
For almost all of the questions, I was asked to write code and optimize it.
ROUND 2: INTERVIEW 1: Technical
- Write solid secure code to generate the power set of a given set of elements:
Eg: If input A={1,2,3}, result= {(1),(2),(3),(1,2),(1,3),(2,3),(1,2,3),(NULL)}
- Write a linear time algorithm to find all combinations of given sets.
Eg: If input = {1,2} ,{3,4} and {5,6},
Output:
{{1 3 5},{2 3 5},{1 4 5 },{2 4 5},{1 3 6},{2 3 6},{1 4 6},{2 4 6}}
Optimize the algorithm to the maximum possible extent. Prove mathematically that it is optimal.
- How do you create a random number generator? (Note: Not Pseudorandom numbers)
- If you are asked to design the next version of Bing, say Bing 2.0, how do you start?
- What are the features that will be added/modified/removed
- How can you make it better than the other search engines
- How do you implement spell check in a search engine: eg: If you search “Maximm”, the search engine shows “Did you mean Maximum?”. How do you implement this feature? How can you use the feature for proper nouns?
- The Interviewer then started digging deep down with questions on the nuts and bolts of the data structures and data-statistics tools that are used for search engine design. (This took a looong time J )
- How will you design a spell checker for MS Word? How is it different from that of Bing? Write Code
- Write a program to delete the nth node from a doubly linked list. Optimize it and verify optimization mathematically.
ROUND 3: INTERVIEW 2: Technical
- Merge two linked lists. Write as many test cases as possible (Preferably around 20)
- Analyze the logic patterns of inputs in the merging problem. How can we take advantage of the patterns?
- Which is your most favorite project? Explain.Code.Optimize.
- Write Test cases based on it.
- The Interviewer started with Operating System concepts and started chaining an answer to the successive questions. It went on for a while: DeadLocks->Algorithms for DeadLock prevention(WriteCode)->Operating System security->Security domains->Semaphores(WriteCode)->InterProcess Communication->ProducerConsumer Problem(WriteCode)->Syncronization problem(WriteCode)->Testing methods
ROUND 4: INTERVIEW 3: Technical
- How do you setup a networking infrastructure (hardware) which incorporates multiple servers, all offering different services, like email, business processing, etc. such that ,if the clients can use just 1 login- info to access a multitude of services.
- Write test cases
- How to solve Synchronization problem(Write code )
- What are the Error recovery mechanisms
- Swap the even-Odd positions in a doubly linked list. Swap the nodes, not just the values in them.
Example:
- I design a program called “copy.exe” which accepts 2 command line arguments ‘source’ and ‘destination’. What are the test cases that are to be considered? Analyze the situation completely.
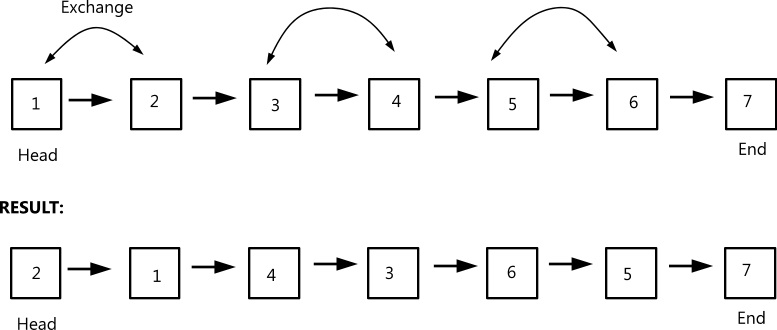
ROUND 5: INTERVIEW 4: Technical
He asked me what my area of interest is, to which I replies ‘Information Security’. The following 2 hours were completely about info-security.
- How to encrypt a message that is to be sent from A to B, when B doesn’t know the key. The Messenger carries the message from A to B. He can travel from A to B and back to A. He carries only the message and not the key. Find a scheme to make sure that the messenger won’t be able to read the msg that he carries, and that the msg reaches its destination safely.
- Debug the following: He gave me sheets with codes printed on them and asked me to debug the same. After debugging all errors, I was asked to code a fair copy of the same.
- Reversing a linked list
- Inserting a node into a linked list
- Sorting a doubly linked list
- Write a program to delete a node from a linked list
- Optimize the programs that you write.
- How to use chaos theory in encrypting messages: Faigenbaum Numbers, U-Sequence, Deterministic unpredictability, White noise.
The Interview was an amazing experience. It was of a kind that I’ve never experienced before. The Questions were so different that we lost track of time.
Thanks for your time,
Vignesh Murugesan,Amrita School of Engineering.
My Twitter ID: http://twitter.com/vignesh_wiz
Facebook Page: http://facebook.com/vignesh.murugesan.me
Placed at Microsoft IDC
I am a student of Amrita University, a peaceful university in tamil nad with an enthusiastic set of faculty members. Being an MSP, Microsoft Student Partner, I was given a shot at an interview for a Dev @ MS Hyderabad. After a written round and four successive interviews, I got a mail from Microsoft stating that they are offering me a job with a good salary package. I ve decided to take it up…
Microsoft IDC
CodeJam: Theme Park code
Problem C:
Roller coasters are so much fun! It seems like everybody who visits the theme park wants to ride the roller coaster. Some people go alone; other people go in groups, and don’t want to board the roller coaster unless they can all go together. And everyone who rides the roller coaster wants to ride again. A ride costs 1 Euro per person; your job is to figure out how much money the roller coaster will make today.
The roller coaster can hold k people at once. People queue for it in groups. Groups board the roller coaster, one at a time, until there are no more groups left or there is no room for the next group; then the roller coaster goes, whether it’s full or not. Once the ride is over, all of its passengers re-queue in the same order. The roller coaster will run R times in a day.
For example, suppose R=4, k=6, and there are four groups of people with sizes: 1, 4, 2, 1. The first time the roller coaster goes, the first two groups [1, 4] will ride, leaving an empty seat (the group of 2 won’t fit, and the group of 1 can’t go ahead of them). Then they’ll go to the back of the queue, which now looks like 2, 1, 1, 4. The second time, the coaster will hold 4 people: [2, 1, 1]. Now the queue looks like 4, 2, 1, 1. The third time, it will hold 6 people: [4, 2]. Now the queue looks like [1, 1, 4, 2]. Finally, it will hold 6 people: [1, 1, 4]. The roller coaster has made a total of 21 Euros!
Input
The first line of the input gives the number of test cases, T. T test cases follow, with each test case consisting of two lines. The first line contains three space-separated integers: R, k and N. The second line contains N space-separated integers gi, each of which is the size of a group that wants to ride. g0 is the size of the first group, g1 is the size of the second group, etc.
Output
For each test case, output one line containing “Case #x: y”, where x is the case number (starting from 1) and y is the number of Euros made by the roller coaster.
Limits
1 ≤ T ≤ 50.
gi ≤ k.
Small dataset
1 ≤ R ≤ 1000.
1 ≤ k ≤ 100.
1 ≤ N ≤ 10.
1 ≤ gi ≤ 10.
Large dataset
1 ≤ R ≤ 108.
1 ≤ k ≤ 109.
1 ≤ N ≤ 1000.
1 ≤ gi ≤ 107.
Sample
Input:
3
4 6 4
1 4 2 1
100 10 1
1
5 5 10
2 4 2 3 4 2 1 2 1 3
Output:
Case #1: 21
Case #2: 100
Case #3: 20
My Solution:
//”Live Live King Size”
#include<string>
#include<fstream.h>
#include<iostream.h>
class queue
{
int n,lead;
long long double g[1001];
public:
queue()
{}
queue(int len,long long double garr[1001])
{
n=len;
for(int i=0;i<1001;i++) g[i]=garr[i];
lead=-1;
}
long long double peek()
{
return(g[0]);
}
void plop()
{
long long double temp=g[0];
int i=0;
for(i=0;i<n-1;i++) g[i]=g[i+1];
g[i]=temp;
}
};
long long double solve(int n,long long double g[1001],long long double r,long long double k)
{
queue q(n,g);
long long double cash=0;
for(long long double z=0;z<r;z++)
{
long long double cap=0,ploprest=0;
for(int zi=0;zi<n;zi++)
{
if(((cap+q.peek())<=k)&&(ploprest==0))
{ cap+=q.peek();
cash+=q.peek();
q.plop();
}
}
}
return cash;
}
int main()
{
ifstream x;
x.open(“q.in”);
ofstream y;
y.open(“a.in”);
long long double man;
int T;
x>>T;
cout<<“\nTCases : “<<T;
//int solve(int n,int g[1000],int r,int k)
int n;
long long double r,k,ans;
int Tcount=1;
long long double g[1001]={0};
while(Tcount<=T)
{
cout<<“\n”<<“Test case: “<<Tcount;
x>>r;
x>>k;
x>>n;
for(int ncounter=0;ncounter<n;ncounter++)
x>>g[ncounter];
ans=solve(n,g,r,k);
cout<<“\nans: “<<ans;
y<<“Case #”<<Tcount<<“: “<<ans<<“\n”;
Tcount++;
}
x.close();
return 0;
}
Vignesh Murugesan's Blog 